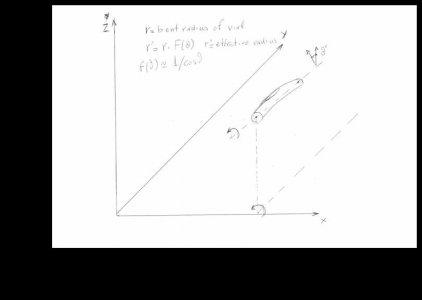
First i would like to thank you for encourage and good words.I have made a free hand sketch to explain the idea.
View attachment 99175
I am using a Bent Vial. If you rotate the vial around an axis parallel to the diameter of bending,the effective radius,and
therefor the sensitivity,will vary.The effective radius will go from initial bending radius to infinity for a rotation of the
vial (angle θ) from zero to 90 degrees.The sensitivity can be defined as a= l/r where l is the movement of the bubble and
r is the effective radius of the vial.I have arrived at a grafic solution for the expression of F(θ) but the analytical solution
escapes me at the moment.I have to express the radius of curvature of an ellipse at the point of minor semiaxis intersection
to the periphery as θ increases.The ellipse is the projection of the vial circle to the XY plane.It has the major axis constant,that
is the diameter of the bending circle an the minor semiaxis goes from r to zero analogus to cosθ as the vial is rotated. In the
end ,at 90 rotation,this ellipse reduces to a straight line and therefor the effective radius goes to infinity.
An approximate expression for F(θ) might be as in the sketch above.
Anyway if calibration is done after construction by an indepented means(e.g. a sine bar) it has a small significance,
but is satisfactory for the completeness of the solution.
I hope that this small presentation is clear enough.I will await your comments.
Ariscats