One of the tricky things about "counting fringes" to determine deviation from flatness is that you can't determine if the fringes are due to high spots or low spots. The fringes arise from the absolute value of the path length difference between the flat and surface it's resting on. A minimum-intensity reflection occurs when the path length difference is one half the wavelength of incident light, and since the light passes through the gap and then bounces back through the same distance, that means the _actual_ path length difference is a multiple of one quarter-wavelength. Notice the "multiple of" caveat. You don't know how many -- the actual distance could be .25*lambda, 1.25*lambda, 2.25*lambda.....etc.
So if you count fringes between point A and point B you can say something about the variation in the flatness between them, but you don't know where they started from, and you don't know if A is higher or lower than B. You CAN say that the surface is flat to some value, and that often is good enough.
But suppose what you really want is a way to make your surface flatter. If you know what regions are higher, and by how much, you can selectively polish those areas and thus refine the surface. Much like scraping but more quantitative, and capable of producing REALLY flat surfaces. This is called "deterministic polishing" and is used in the optics industry for making extremely fine optics. Things like lambda/100 stuff.
There is a tricky way to eliminate the higher/lower ambiguity. I used a variation of it to develop my own version of a deterministic polishing system for doing failure analysis on integrated circuits. Hopefully the two included figures and vigorous arm-waving on my part will explain it

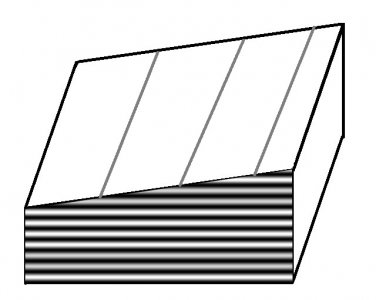
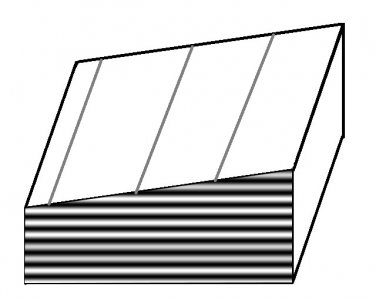
In both figures I'm showing the gap between a flat and the surface it's resting on. The light/dark horizontal bands show the locations of dark fringes in space. The vertical bands show the fringes that are created when the reflected light from the surface interferes with the light bouncing off the optical flat. Note the change in the positions of the fringes between the two figures. The difference is that the wavelength of light for the left-hand figure is slightly shorter than the right-hand side. It's not obvious unless you download these into a separate folder and then flip between them, but this shows that the fringes move FROM the widest gap when the wavelength decreases. Thus by slightly changing the wavelength of our light source the height vs depth ambiguity has been eliminated. However we STILL don't know the actual path length difference: but now we can refine the surface if we want to do so.
This seems to beg the question, "how can we slightly change the wavelength of our light source?". And the answer is to use your common LED's wavelength vs. temperature dependence. When a red LED gets hotter its bandgap decreases (see
here for an explanation). So its wavelength increases. Conversely, its wavelength decreases as its temperature decreases. The best way to manage an LED in this fashion would be to use a thermoelectric cooler, with a purchased or home-made PID controller.
For a really nifty result you can make a series of photos taken with different LED temperatures and quickly page-flip through them to make a little movie of the fringes moving. In my case I wasn't changing the color of an LED (I was using a fixed-wavelength laser) but it so happens that silicon's index of refraction has a very strong temperature dependence. So by changing the temperature of the silicon I changed the effective path length, and the fringes moved as predicted.


